Una simple baldosa (I)

Lo sencillo es bello y, a la vez, profundo.

Esta historia comienza a principios del siglo XVIII, de la mano de un cura dominico francés, Sébastien Truchet, que se interesa por los patrones de las baldosas de cerámica decorativas de los canales franceses que había diseñado. A partir de una baldosa dividida por la diagonal, con una de sus mitades de color se dedica a estudiar los posibles entramados que se pueden crear con ella. De la combinación de tan solo dos baldosas con las 4 rotaciones y en las 4 posiciones relativas posibles, ya se generan 54 patrones que Truchet agrupa en 10 formas distintas de combinaciones.

Baldosa de Truchet

Las posibles combinaciones son virtualmente infinitas y algunos de ellos, generalmente los que poseen algún tipo de simetría nos llevan acompañando toda la vida. Animo al lector a que emule a Truchet y estudie qué combinaciones se pueden conseguir creando cuadrados de 2x2 o de 3x3 baldosas y cuáles son visualmente atractivas.

Imágenes obtenidas de la Wikipedia. 

Casi 300 años después, un ingeniero metalúrgico, pieza importante del proyecto Manhattan y profesor de universidad, Cyril Stanley Smith, escribe un artículo relacionado con las baldosas de Truchet y su relación con los defectos en materiales. En el artículo, introduce también un diseño sencillo de baldosa pero que combinándolo entre sí, consigue un entramado de zonas abiertas y cerradas muy llamativo.

Baldosa de C.S.Smith

La combinación de estas u otras baldosas con similar filosofía ha dado lugar a una infinidad de composiciones denomidadas Teselaciones de Truchet. En algunos casos, el resultado obtenido es un laberinto cuyas propiedades se pueden estudiar por Teoría de percolados.

Baldosa usada para
el Laberinto de truchet

En otros casos, se puede crear un patrón de carreteras, cruces y rotondas que invita a buscar el camino más corto entre dos puntos.

Baldosas utilizadas para, lo que podemos denominar,
la ciudad de truchet

Creación de nuevas baldosas

Resulta muy estimulante pensar qué otras baldosas se podrían diseñar (por ejemplo, las de Smith pero con rectas en vez de curvas, o las originales de Truchet, con curvas en vez de rectas,...) y catalogarlas por el número de líneas que contienen o por el número de regiones que forman. Además, todas ellas pueden ser susceptibles de ser coloreadas, o bien por sus áreas o bien por sus líneas. dando pié a baldosas bitonales, tritonales, tetratonales...

Compilación de baldosas mencionada más alguna nueva
y su coloración tanto de líneas como de áreas.

Truchet en 3D

La baldosas 2D de Truchet se han adaptado al espacio tridimensional en el que la celda unidad es un cubo.

Ejemplo de cubo de Truchet
Renderizado por Paul Bourke

Truchet Tile In 3D from RINBOKU on Vimeo.

Baldosas con otras formas

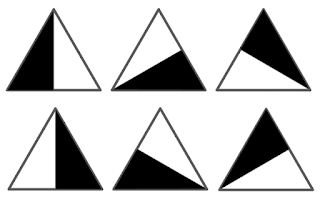
Pero por si esto no fuera suficiente, se puede imaginar otro tipo de baldosa no cuadrada que cubra todo el espacio 2D, por ejemplo triángulos, pentágonos, hexágonos,... y diseñar para esas figuras baldosas y teselaciones de Truchet. Aquí os dejo algunos desarrollos que he realizado para el caso de triángulos equiláteros y un caso de baldosas de Truchet para hexágonos comerciales que pertenecen al juego abstracto Tantrix.

Baldosas triangulares tipo Truchet

Teselación de Truchet triangular aleatoria
formando hexágonos

Teselación de Truchet triangular con
patrón definido apilada

Baldosas del juego Tratrix

En esta primera entrada sobre el tema queda patente el potencial casi infinito de la idea subyacente a una sencilla baldosa y su repercusión en el diseño de cientos de objetos. En la siguiente entrada hablaré de los usos actuales o futuribles de este tipo de baldosas en los juegos de mesa que es lo que nos conciernen en este blog.

Referencias

La idea original de este post surgió de la siempre interesante web de Math Munch y múltiples entradas de la Wikipedia.